在测量压力时要考虑很多因素。其中当然包含介质的实际属性。
其中最基本的区别在于介质是可压缩还是不可压缩性。可压缩性介质是一种密度和体积都与压力有关的物质,如气体。而不可压缩介质,无论压力大小,体积恒定,诸如液体。然而,应该注意的是,不可压缩性是一种理想状态,在现实中是不存在的。然而,水或液压油之类的液体在实践中被称为不可压缩介质,因为采用第一近似它们是不可压缩的。假设在正常条件下,管道内的水是不可压缩的,因为这极大地简化了运算,任何产生的误差都可以忽略不计。
我们以体积流量的计算为例。因为液体是不可压缩的,即它们的密度不变,如果体积恒定时(和由此带来的压力变化),断面流速扩大或缩小,就可适用以下公式:
Q = A1 •v1 = A2 •v2
由于气体的可压缩性则不适用于此公式。
由此可推测:静力学和动力学之间的差异在这里也很重要。静力学表示力的平衡。在这种情况下,由于压力差的均衡,不会出现流动现象。
而动力学则是完全不同的。在本例中,我们区分不同类型的流动现象。
- 稳定流动: 当流速不随时间变化而始终保持稳定的情况下存在稳定流。
- 瞬态流动: 瞬态流动会随着时间的变化而产生。比如泵和阀孔。它可以从动态点直接冲到压力峰值,因此也会损坏管道。
- 层流: 在层流中,流体在非混合层中流动。这里没有紊流,每层流速都不同。
摩擦也起着重要的作用。这里会发现外部摩擦和内部摩擦之间的区别。前者指的是流体和触面之间的摩擦(比如流体流动的管道内壁).在层流中会发生内部摩擦,例如,单层流体之间的摩擦。作用于流体的摩擦力取决各种参数,需要复杂的计算。这些参数包括内壁的粗糙度,流速,密度和粘度。后者也依赖于温度,这就进一步复杂了最终的计算。
现在回到静力学和动力学的区别。当我们试图建立重力压力时我们谈到了静态压力测量(也称为静水压力)。这指的是在万有引力作用下流体产生的压力。例如,测量静水压力用以检测罐体内的液位。在这里,可压缩介质和不可压缩介质的区别是很重要的,因为水的静水压力的计算比可压缩气体要容易得多。
不可压缩介质的质量等于它的密度乘以它的体积,也等于密度乘以面积,乘以高。对于计算静水压力,我们使用:
p = F/A = ρAhg/A = ρgh
p = 压力
F =力
A = 面积
ρ = 密度
h = 高
g = 重力
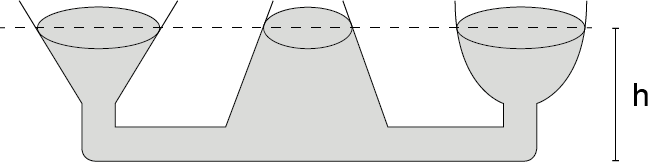
这个公式里的压力和介质深度程正比例。容器的形状或横截面积在这里不起任何作用。因此,静水压力与容器内的体积无关,而是与填充高度有关。这种现象也被称为流体静压佯谬。